I was struggling with sqlcl on Windows 7 to properly display our umlauts (we’re using Windows 7 desktops with NLS_LANG=SLOVENIAN_SLOVENIA.EE8MSWIN1250 setup in the registry — note: sqlcl is not reading this variable).
When I read Jeff Smith blog post “Unicode and Oracle SQLcl…on Windows” I though that my problem was solved. Someone reading an article without reading the comments would assume that sqlcl works out of the box on Windows with proper UTF-8 support, which does not. Partly due to the omission of proper parameter in supplied sql.bat file, but mostly because of the state of cmd.exe (powershell.exe) in versions of Windows 7 and below, Windows 10 is much better.

In this demo we’re using Windows 7 EE (Windows 10 EE), Oracle 12c R1 and sqlcl-4.2.0.16.308.0750-no-jre.zip.

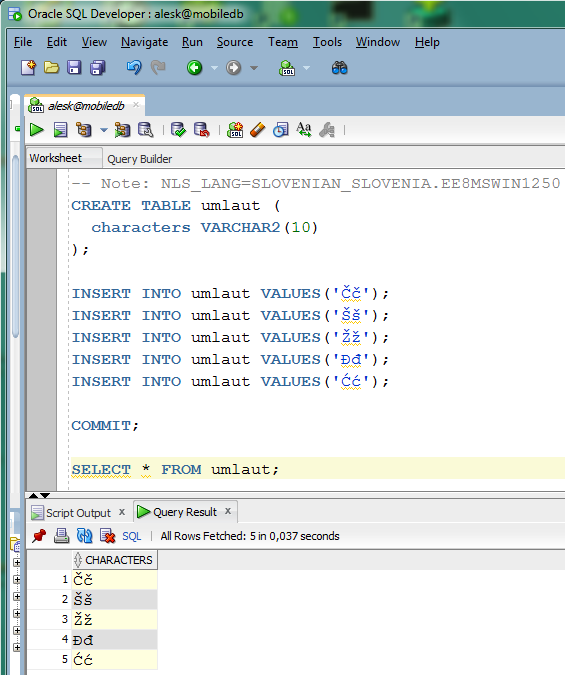
First, we created test table called UMLAUT in SQL*Developer and inserted our umlauts:

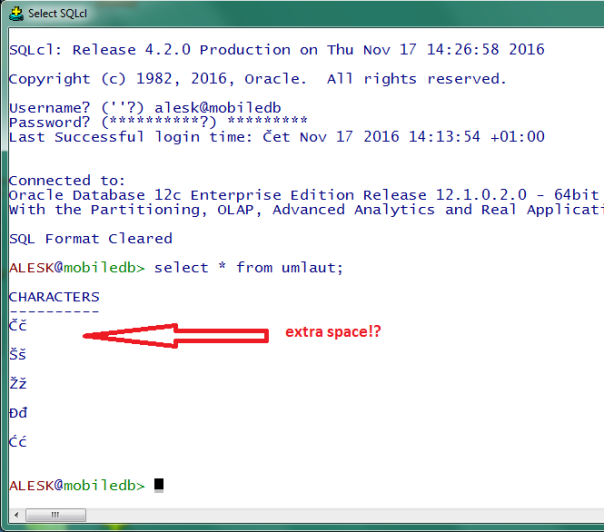
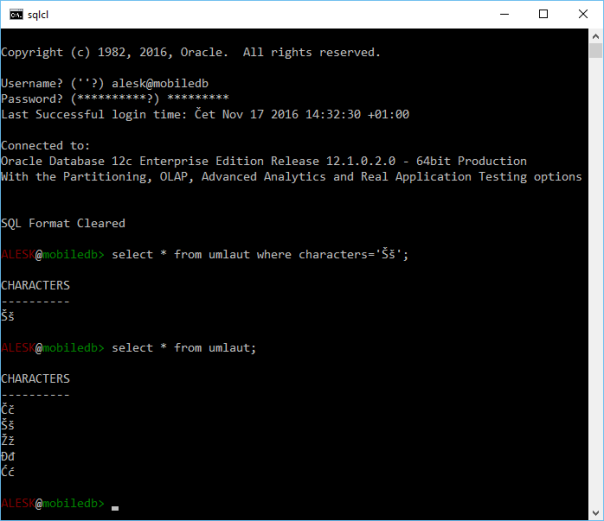
Then we run a query from this table with sqlcl. Note an extra line between the rows returned from the query….

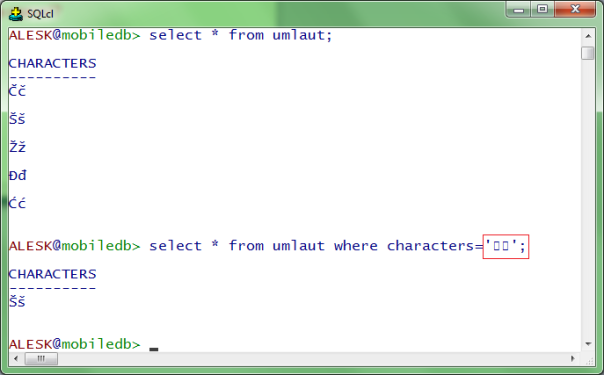
ok, how about writing some umlauts on the command line….

Well, we can write umlauts but console won’t show us what we wrote (note a presence of squares)…nevertheless the result of the query is correct.

What we can do? Well, for a start we need to patch the officially supplied sql.bat script.

Open sql.bat and replace line

SET STD_ARGS=-Djava.awt.headless=true -Xss10M

with

SET STD_ARGS=-Djava.awt.headless=true -Xss10M -Dfile.encoding=UTF-8

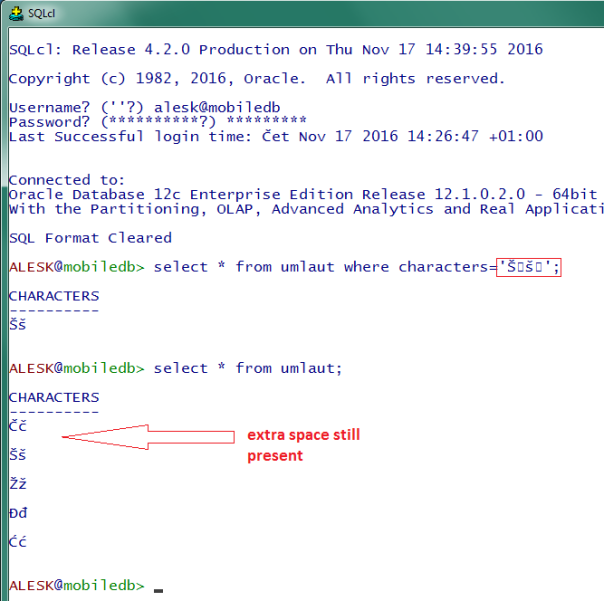
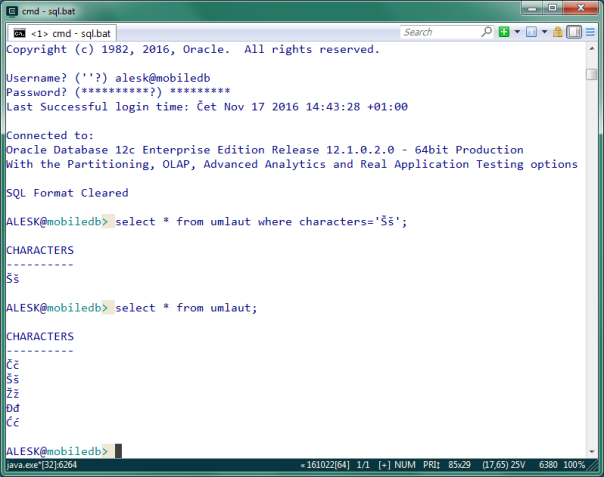
But don’t celebrate yet…what we achieved is this….

We still have an extra line between the rows, which is annoying, but at least we can see what we wrote in the WHERE condition. Plus an extra square :-)…if you’re “lucky” Windows 7 user.
However, above patch is enough on Windows 10, where, both writing of umlauts and properly displaying the records (without extra blank line) works as expected….

The only “workaround” that we found for Windows 7 clients is to simply forget about official console applications (cmd.exe and powershell.exe) as a “host” for sqlcl and use some alternative. We found out that ConEMU works great…(patch in the sql.bat is of course still mandatory until sqlcl guys do this for you).

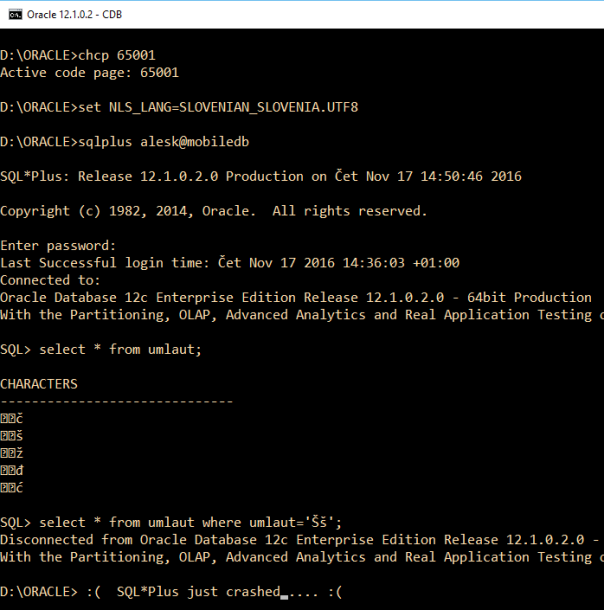
And what about the suggestion that we can tweak the registry and permanently change the console application (cmd.exe) code page to UTF? Don’t do this, because you’ll disable some non-java applications, including SQL*Plus…look what happens with sqlplus.exe….